Vihje 1: Miten määrität kolmion tyypin
Vihje 1: Miten määrität kolmion tyypin
Kolmiosa on yksinkertaisin monikulmio. Se koostuu kolmesta pisteestä, jotka sijaitsevat yhdessä tasossa, mutta ei yhdestä suorasta viivasta, jotka on yhdistetty pareittain segmentteihin. Kolmiot voivat kuitenkin olla melko erilaisia, ja sen seurauksena niillä on erilaiset ominaisuudet.
opetus
1
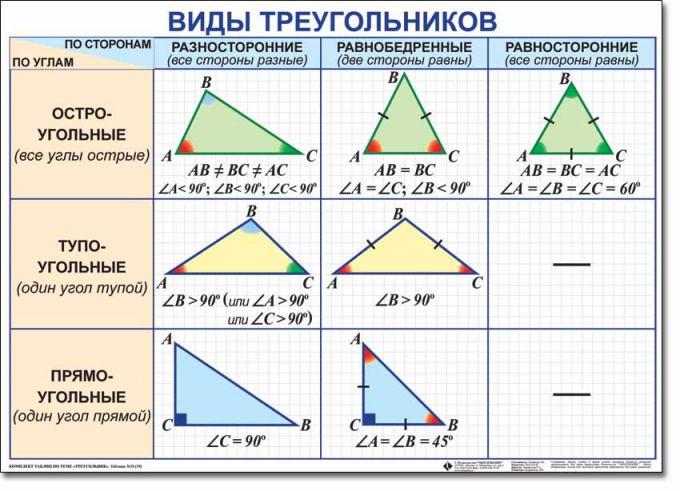
On tavallista erottaa kuusi laji kolmioita. Tämän divisioonan ytimessä on kaksi luokitusta: kulmissa ja sivuilla. Luokittelu luokkakulmien mukaan edellyttää kolmioiden jakautumista akuuttiin, suorakulmaiseen ja tylppäiseen. Sivuryhmien luokittelu jakaa kolmiot monikäyttöisiksi, tasavertaisiksi ja isosceleksi. Ja jokainen kolmio samanaikaisesti kuuluu kahteen tyyppiin. Esimerkiksi se voi olla suorakulmainen ja monipuolinen samanaikaisesti.
2
Määritellään lomake kolmio kulmien tyypin mukaan, oltava erittäin varovainen. Kutsu on tylppä kolmio, jossa yksi kulmista on tylppä, eli yli 90 astetta. Suorakulmainen kolmio voidaan laskea yhden suora (90 asteen kulmalla) kulman perusteella. Kuitenkin, jotta kolmio voidaan luokitella akuutiksi, sinun on varmistettava, että kaikki kolme sen kulmaa ovat terävät.
3
Määritellään lomake kolmio sivusuhde on ensin sinun täytyyoppia kaikkien kolmen puolen pituudet. Jos kuitenkin osapuolten pituuden kuntoa ei anneta, kulmat voivat auttaa sinua. Monipuolinen on kolmio, jonka kaikki kolme puolta ovat eri pituisia. Jos sivujen pituudet ovat tuntemattomia, kolmio voidaan luokitella monikäyttöiseksi, jos kaikki kolme sen kulmaa ovat erilaiset. Monipuolinen kolmio voi olla tylppä, suorakulmainen ja akuutti.
4
Isosceles kolmio, kaksi niistäjonka kolme puolta ovat yhtä suuret kuin toiset. Jos sivujen pituuksia ei anneta sinulle, ohjaa kaksi yhtä suurta kulmaa. Isosceles kolmio, kuten monipuolinen, voi olla sekä tylppä, suorakulmainen ja akuutti kulma.
5
Vastaavaa voi nimetä vainKolmiota, jonka kaikki kolme puolta ovat yhtä pitkiä. Kaikki sen kulmat ovat yhtä suuria kuin toiset, ja jokainen niistä on yhtä suuri kuin 60 astetta. Siksi on selvää, että tasasivuiset kolmiot ovat aina akuutteja kulmia.
Vihje 2: Kuinka tunnistaa tylppä ja akuutti kulma-kolmio
Yksinkertaisin monikulmio on kolmio. Se on muodostettu kolme pistettä yhdessä tasossa, mutta eivät sijaitse yhdellä rivillä paria yhdistetty segmentteihin. On kuitenkin olemassa erilaisia kolmiot ja siksi on erilaiset ominaisuudet.

opetus
1
On tavallista erottaa kolmentyyppiset kolmiot: tylppä, akuutti ja suorakulmainen. Tämä on luokittelu kulmien tyypin mukaan. Tuttu kolmio on sellainen, jossa yksi kulmista on tylppä. Blunt on kulma, joka on yli yhdeksänkymmentä astetta, mutta alle sata ja kahdeksankymmentä. Esimerkiksi, että kolmion ABC ABC kulma on 65 °, BCA kulma on 95 °, kulma CAB on 20 °. Kulmat ABC ja CAB ovat alle 90 °, mutta kulma BCA on suurempi, joten kolmio on tylppä.
2
Akuutti kolmio on kolmio, jonkakaikki kulmat ovat teräviä. Terävä kulma on kulma alle yhdeksänkymmentä ja suurempi kuin nolla astetta. Esimerkiksi kolmion ABC kulmassa ABC on 60 °, kulma BCA on 70 °, kulma CAB on 50 °. Kaikki kolme kulmaa ovat alle 90 °, joten kolmio on äkillinen kulma. Jos tiedät, että kolmion kaikki sivut ovat yhtä suuria, tämä tarkoittaa, että kaikki sen kulmat ovat yhtä suuria toisiaan vasten, kun ne ovat yhtä kuin kuusikymmentä astetta. Näin ollen kaikki kulmat tällaisessa kolmiossa ovat alle yhdeksänkymmentä astetta, ja näin ollen tällainen kolmio on akuutti kulma.
3
Jos kolmiossa yksi kulmista on yhtä suuri kuin yhdeksänkymmentä astetta, tämä tarkoittaa sitä, että se ei koske laajakulmityyppiä tai akuuttia kulmaa. Tämä on oikean ankkuroitu kolmio.
4
Jos kolmion muoto määräytyy suhteen mukaanosapuolet, ne ovat tasa-arvoisia, monipuolisia ja isosceles. Tasapainotteisessa kolmiossa kaikki sivut ovat yhtä suuria, ja tämä, kuten löysit, osoittaa, että kolmio on akuutti kulma. Jos kolmiossa on vain kaksi puolta tai sivut eivät ole yhtä suuria kuin toiset, se voi olla tylppä, suorakulmainen ja akuutti. Näin ollen näissä tapauksissa on tarpeen laskea tai mitata kulmia ja tehdä johtopäätöksiä 1, 2 tai 3 kohdan mukaisesti.
Vihje 3: Mitkä kolmioita kutsutaan tasavertaisina
Kahden tai useamman kolmion yhtäläisyys vastaa tapausta, jossa kaikkien näiden kolmioiden sivut ja kulmat ovat yhtä suuret. On kuitenkin olemassa useita yksinkertaisempia kriteerejä tämän tasa-arvon osoittamiseksi.

Tarvitset
- Oppikirja geometriasta, paperiarkista, yksinkertaisesta kynästä, hammaspyörästä, viivain.
opetus
1
Avaa seitsemäs asteen geometrian oppikirjakohta kolmikulmien tasavertaisuuden merkistä. Näet, että on olemassa useita perusominaisuuksia, jotka osoittavat kahden kolmion tasavertaisuuden. Jos kaksi kolmioa, joiden tasa-arvo todetaan, ovat mielivaltaisia, niin heille on olemassa kolme tasavertaista tasa-arvoa. Jos kolmiota koskevia lisätietoja on tiedossa, tärkeimpiä kolmea ominaisuutta täydentävät useat muut. Tämä pätee esimerkiksi tasa-arvokulmien tasa-arvoon.
2
Lue ensimmäinen sääntö tasa-arvostakolmioita. Kuten tiedät, sen avulla voit tarkastella kolmiota yhtä paljon, jos pystyt osoittamaan, että kahden kolmion kulma ja kaksi vierekkäistä sivua ovat yhtä suuret. Jotta ymmärtäisit tämän lain toimivuuden, vedä paperiarkki, jossa on kulmamittari, kaksi samanlaista määritettyä kulmaa, jotka muodostuvat kahdesta säteestä, jotka ovat peräisin yhdestä pisteestä. Mittaa hallitsija samoilla sivuilla vedetyn kulman päältä molemmissa tapauksissa. Käytä mittapistettä mittaamalla kahden muodostetun kolmion kulmat, varmista, että ne ovat yhtä suuret.
3
Jotta ei käytetä tällaisia käytännöllisiätoimenpiteet kolmion tasa-arvon ymmärtämiseksi, lue tasa-arvon ensimmäisen merkin todistus. Tosiasia on, että jokaisella kolmikulmien tasa-arvolla on tiukka teoreettinen todiste, ei ole yksinkertaista käyttää sitä sääntöjen muistamiseen.
4
Lue toinen merkki kolmikulmien tasa-arvosta. Se toteaa, että kaksi kolmioa ovat yhtä suuret, jos kummallakin puolella ja kahdella vierekkäisellä kulmalla kaksi tällaista kolmiota ovat yhtä suuret. Jotta voisit muistaa tämän säännön, kuvittele kolmion ja kahden vierekkäisen kulman vedetty puoli. Kuvittele, että kulmien sivupituudet kasvavat asteittain. Lopulta ne leikkaavat, muodostaen kolmannen kulman. Tässä henkisessä tehtävässä on tärkeää, että henkisesti kasvavien sivujen leikkauspiste sekä tuloksena oleva kulma määritetään yksitellen kolman- nella osapuolella ja kahdella vierekkäisellä kulmalla.
5
Jos et ole saanut tietoa kulmistakäytä kolmatta kolmiota tasa-arvoista merkkiä. Tämän säännön mukaan kaksi kolmioa pidetään yhtä suurina, jos jokin niistä on kolmella sivulla yhtä suuri kuin toisen vastaava kolme sivua. Siten tämä sääntö kertoo, että kolmion sivujen pituudet määräävät yksiselitteisesti kaikki kolmion kulmat ja siksi ne yksiselitteisesti määrittävät kolmion.







