Vihje 1: Miten löytää toiminnon nollat

tiede

Vihje 1: Miten löytää toiminnon nollat

Funktion matemaattinen käsite osoittaaon ilmeistä, kuinka yksi arvo määrittää kokonaan toisen määrän arvon. Yleensä numeerisia toimintoja pidetään, jotka asettavat yhden numeron toiselle. Toiminnon nollaa kutsutaan yleensä argumentin arvoksi, jossa funktio on nolla.

opetus

Toiminnon nollien löytämiseksi on tarpeen tasata sen oikea puoli nollaksi ja ratkaista tuloksena oleva yhtälö. Oletetaan, että annetaan funktio f (x) = x-5.

Tämän toiminnon nollojen löytämiseksi otamme sen oikean puolen nollaan: x-5 = 0.

Tämän yhtälön ratkaisemiseksi saadaan x = 5 ja argumentin u tämä arvo on funktion nolla. Eli argumentin 5 arvoilla funktio f (x) häviää.

Vihje 2: Toiminnon arvon löytäminen

Käsitteen mukaan tehtävät matematiikassa ymmärtää elementtien välistä suhdettasarjaa. Tarkemmin sanottuna tämä on "laki", jolla jokainen elementti (kutsutaan määritelmän domeeni) liittyy johonkin toiseen joukkoon (jota kutsutaan arvoalueeksi).

Tarvitset

Algebrassa ja matemaattisen analyysin osaaminen.

opetus

merkitys tehtävät tämä on tietty alue, arvot, joista funktio voi ottaa. Esimerkiksi arvoalue tehtävät f (x) = | x | 0: stä ääretön. Löytää merkitys tehtävät on tietyssä vaiheessa korvattava argumentin sijasta tehtävät sen numeerinen vastaava, tuloksena oleva luku on merkitysm tehtävät. Antaa funktion f (x) = | x | - 10 + 4x. Me löydämme merkitys tehtävät pisteessä x = -2. Korvataan numero -2: x: f (-2) = | -2 | - 10 + 4 * (- 2) = 2 - 10 - 8 = -16. Se on merkitys tehtävät -2: ssa se on -16.

Vihje 3: Miten määrität toiminnon nollat

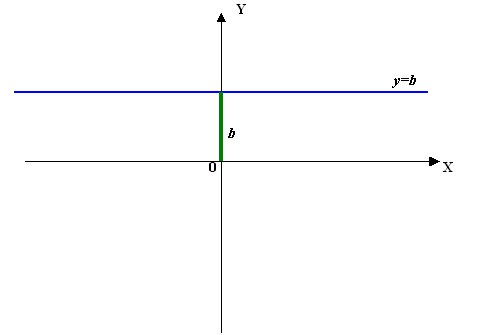
Toiminto on vakiintunutmuuttujan y riippuvuus muuttujasta x. Jokaisen x: n arvo, jota kutsutaan argumentiksi, vastaa y-funktion yhtä arvoa. Graafisessa muodossa funktio on kuvattu karteesiläisellä koordinaatistojärjestelmällä kaavion muodossa. Kaavion leikkauspisteet abskissa, jossa argumentit x on piirretty, kutsutaan funktion nolliksi. Mahdollisten nollien etsiminen on yksi tehtävän tutkimisesta. Tässä otetaan huomioon kaikki mahdolliset riippumattoman muuttujan x arvot, jotka muodostavat funktiomäärityksen (OOF) verkkotunnuksen.

opetus

Toiminnon nolla on argumentin x arvo,jossa funktion arvo on nolla. Kuitenkin vain ne argumentit, jotka tulevat tutkittavan funktion alueelle, voivat olla nollia. Eli sellaisessa arvoryhmässä, johon funktio f (x) on järkevää.

Merkitse määritetty toiminto ja osoita senolla, esimerkiksi f (x) = 2h² + 5h + 2 = 0. Ratkaise tuloksena oleva yhtälö ja etsi sen todelliset juuret. Neliöllisen yhtälön juuret lasketaan etsimällä erottelukyky. 2h² + 5x + 2 = 0, D = b²-4ac = 5²-4 * 2 * 2 = 9; x1 = (-b + VD: n funktiona) / 2 * a = (-5 + 3) / 2 * 2 = -0 5, x2 = (-b-VD: n funktiona) / 2 = a * (-5-3) / 2 * 2 = -2.Takim, tässä tapauksessa on valmistettu kaksi juuret asteen yhtälön, joka vastaa väitteet alkuperäinen funktio f (x ).

Etsi kaikki x-arvotjotka kuuluvat tietyn funktion määritelmän alueeseen. Etsi OOF, tarkista täten alkuperäinen ilmentymä yhtälön numeroiden juurille √f (x), funktion fraktioiden esiintymiseksi nimittäjän argumentilla, logaritmisten tai trigonometristen lausekkeiden läsnäolon osalta.

Tarkastellaan funktiota, jonka ilmaus on juuressaedes taso, ota määritelmän verkkotunnukseksi kaikki argumentit x, joiden arvot eivät käännä radikaalia negatiiviseksi numeroksi (muuten toiminto ei ole järkeä). Määritä, onko funktion havaitut nollat asetettu tiettyyn mahdolliseen x: n arvoon.

Fraktion nimittäjä ei voi nollata,joten poista nämä argumentit x, jotka johtavat tähän tulokseen. Logaritmisten määrien osalta on otettava huomioon vain ne argumentin arvot, joille itse ilmentymä on suurempi kuin nolla. Toiminnon nollat, jotka kääntävät logaritmisen ilmentymisen nollaksi tai negatiiviseksi, on hylättävä lopullisesta tuloksesta.