Miten löytää trapetsin pohja, jos sivu ja kulma ovat tiedossa
Miten löytää trapetsin pohja, jos sivu ja kulma ovat tiedossa
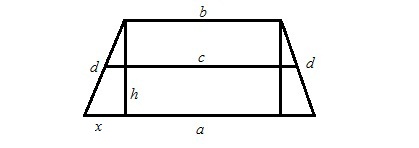
Trapezium on tietty nelikulmio. Kaksi tämän kuvion neljästä sivusta on rinnakkaisia ja niitä kutsutaan suuriksi ja pieniksi pohjaksi. Muut kaksi puolta pidetään sivuttaisina.

Tarvitset
- -karandash
- -lineyka
opetus
1
Piirrä mielivaltaisen pituuden säde mistä tahansa pisteestäkoneessa. Oletetaan, että trapetsin pohja sijaitsee tällä säteellä. Lähtöpisteestä piirrä viiva tehtävässä määritetyn kulman alla, joka vastaa puolisuunnikkaan tunnettua puolta. Jos ongelma on ratkaistu yleisellä tavalla, piirroksen suorittamiseksi on mahdollista piirtää käsin mittakokoinen kappale alle 90 asteen kulmassa. Kuitenkin mielivaltaisen kokoinen sivu ja sen kaltevuus puolisuunnikkaan pohjaan ovat yksilöllisesti määritellyt, eivätkä ne voi muuttua.
2
Puolesta päästä vedä palkki,rinnakkain ensimmäisen kanssa. Sinulla on osa trapetsoidusta tunnetulla puolella ja yksiselitteisesti määritellyt kulmat tämän puolen ja trapetsin pohjan välillä. On selvää, että pohjojen tai korkeuden välissä on tiukasti määritelty arvo: h = a * Sin α, jossa h on puolisuunnikkaan korkeus ja a on sivu, α on tunnettu kulma.
3
Onko tehtävän mukaan mahdollista oppia jotain muutatarkasteltava trapetsia ja löytää sen perusta? Sivulta ja toisesta alustasta tulevasta tietystä kulmasta voidaan määrittää tämän sivun ja toisen alustan välinen kulma, koska näiden kulmien summa puolisuunnikossa on aina 180 astetta, mutta emme voi oppia mitään perusrakenteiden koosta.
4
Hyvin hyödyllinen tieto olisipuolisuunnikkaan tai sen keskiviivan lävistäjä. Trapeziumin keskilinja ei ole vain pohjalla samansuuntainen, vaan myös numeerisesti yhtä suuri kuin niiden puolikas, ja tämä ominaisuus antaa mahdollisuuden saada vastauksen kysymykseen perusosan koosta. Tunnetun lävistäjän läsnä ollessa ongelma voidaan vähentää kahden tunnetun kolmion kolmannen puolen löytämiseksi. Mutta tietäen vain kulman ja puolen trapetsia, on mahdotonta ratkaista ongelmaa löytää sen perusta yksiselitteisesti.