LovesTheTeam.com

opetus

1

2

Harkitse kolmio ABD. Sivun AB pituus on yhtä suuri kuin vektorin a moduuli. Anna | A | = sqrt ((ax) ^ 2 + (ay) ^ 2) = a, sitten cosf = ax / sqrt (((ax) ^ 2 + (ay) ^ 2), koska suunta kosinin let määritelty. diagonaalinen BD on pituus p, ja haluttu AD pituus X. Tällöin kosinoruutu, P ^ 2 = a ^ 2 + x ^ 2-2axcosφ. Tai x2 2axcosφ + (a ^ 2-p ^ 2) = 0.

3

Ratkaisut asteen yhtälö: X1 = (2acosf + sqrt (4 (a ^ 2) ((cosf) ^ 2) -4 (a ^ 2-p ^ 2))) / 2 = acosf + sqrt ((a ^ 2) ((cosf) ^ 2) - (a ^ 2-p ^ 2)) == a * ax | sqrt (((ax) ^ 2 + (ay) ^ 2) + sqrt ((((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - ^ 2 + p ^ 2) = AD.

4

Yläosan löytäminen perusteet Aurinko (pituus löytämään ratkaisuja myös nimetty x), jota käytetään moduuli | en | = a, ja toinen diagonaalinen BD = q ja kosinikulmaa ABC, joka on selvästi yhtä suuri kuin (p-p).

5

Kolmio ABC, kjoka, kuten aiemmin, sovelletaan kosini-lause, ja seuraava ratkaisu syntyy. Koska cos (n, p) = - cosf, joka perustuu ratkaisu AD, voimme kirjoittaa seuraavan kaavan korvaamalla p-q: BC = - a * ax | sqrt (((ax) ^ 2 + (ay) ^ 2 ) + sqrt ((((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - ^ 2 + q ^ 2).

6

Tämä yhtälö on neliö ja,Näin ollen sillä on kaksi juuria. Näin ollen tässä tapauksessa on vain valita ne juuret, joilla on positiivinen arvo, koska pituus ei voi olla negatiivinen.

7

PrimerPust vuonna trapetsi AB: n ABCD-puoli annetaan vektorilla a (1, sqrt3), p = 4, q = 6. löytää perusteet trapetsiPäätöslauselma. Yllä olevien algoritmien avulla voimme kirjoittaa: | a | = a = 2, cosφ = 1/2. AD = 1/2 + sqrt (4/4 -4 + 16) = 1/2 + sqrt (13) = (sqrt (13) +1) /2.BC=-1/2+sqrt (-3 + 36 ) = (sqrt (33) -1) / 2.

Tarvitset

• Sivut, pohjat, puolisuunnikkaan keskilinja sekä mahdollisesti sen alue ja / tai kehä.

opetus

1

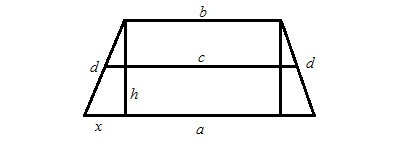
Yksi tapa laskea alueen trapetsiaon korkeuden ja keskilinjan tuote. Oletetaan, että on isosceles trapezoid. Sitten korkeus tasakylkisen puolisuunnikkaan emästen a ja b, alue S ja kehän P lasketaan seuraavasti: h = 2 x S / (P-2 x d). (katso kuvio 1)

2

Jos tunnetaan vain trajektin alue ja sen pohja, korkeuslaskentakaava voidaan johtaa trajektin alueen kaavasta S = 1 / 2h x (a + b): h = 2S / (a ​​+ b).

3

Oletetaan, että on trapetsia, jolla on samat tiedot kuinja kuviossa 1. Piirtäen 2 korkeutta, saamme suorakulmion, jossa kaksi pienempää sivua ovat oikean kulmaisen kolmion jalat. Merkitään pienempi x: lle. Se löytyy jakamalla pituuden ero suurempien ja pienempien emästen välillä. Sitten Pythagoraanin lauseessa korkeuden neliö on yhtä suuri kuin hypotenus d: n ja röntgensäteen neliöiden summa. Poimimme juuren tästä summasta ja saimme korkeuden h. (Kuvio 2)

opetus

1

Tehtävä 1. Etsi BC ja AD suorakaiteen pohjat trapetsijos diagonaalisen AC = f pituus tunnetaan; pituuspuoli CD = c ja kulma sen ADC = α.Reshenie: Tarkastellaan suorakulmaisen kolmion CED. Tunnetut hypotenuusa c ja välinen kulma hypotenuusan ja jalan EDC. Saada pituus puolin CE ja ED: kulma kaava CE = CD * sin (ADC); ED = CD * cos (ADC). Joten: CE = C * sinα; ED = c * cosa.

2

Harkitse oikeaa kolmiota ACE. Hypotenuse AC ja CE ovat tiedossa, löydät sivun AE oikean kolmion säännön mukaan: jalkojen neliöiden summa on yhtä suuri kuin hypotenuksen neliö. Joten: AE (2) = AC (2) - CE (2) = f (2) - c * sina. Laske yhtälön oikean puolen neliöjuuri. Löydit suorakaiteen ylimmän pohjan trapetsi.

3

Perus AD: n pituus on kahden pituuden summasegmentit AE ja ED. AE = neliöjuuri (f (2) - c * sina); ED = c * cosα) Joten: AD = neliöjuuri (f (2) - c * sinα) + c * cosα. trapetsi.

4

Tehtävä 2. Etsi BC: n ja AD: n suorakaiteen pohjat trapetsijos diagonaalin BD = f pituus tunnetaan; pituuspuoli CD = c ja kulma sen ADC = α.Reshenie: Tarkastellaan suorakulmaisen kolmion CED. Etsi CE- ja ED-puolien pituudet: CE = CD * sin (ADC) = c * sinα; ED = CD * cos (ADC) = c * cosa.

5

Harkitse ABCE-suorakulmiota. Suorakulmion AB = CE = c * sinα: n ominaisuus. Tarkastele oikeaa kolmiota ABD. Oikean kolmion omaisuuden mukaan hypotenuksen neliö on yhtä suuri kuin jalkojen neliöiden summa. Siksi AD (2) = BD (2) - AB (2) = f (2) - c * sina. Löysit suorakaiteen trapetsi AD = neliöjuuri (f (2) - c * sina).

6

Suorakulmion sääntö BC = AE = AD - ED = neliöjuuri (f (2) - c * sinα) - c * cosα. trapetsi.

Tarvitset

• - laskin.

opetus

1

Jos tunnetaan kaksi pituutta - suuri pohjatrapezium ja midline - käytä trapezium-ominaisuutta laskemaan pienin pohja. Hänen mukaansa puolisuunnikkaan keskiviiva on sama kuin peruspalkkien puoli. Tällöin pienin pohja on yhtä suuri kuin tämän keskiarvon kaksinkertaisen pituuden ja tämän suuren pohjan pituuden välinen ero.

2

Jos tiedät sellaiset trapetsiset parametrit kuinalue, korkeus, pituus suurella pohjalla, laske sitten tämän pienin pohja puolisuunnikkaan alueen kaavan mukaan. Tässä tapauksessa, lopullinen tulos on saatu vähentämällä erotuksen kaksi kertaa yksityinen alue ja korkeus tällaisen parametrin pituus suuri puolisuunnikkaan pohja.

3

Pienimmän sivun pituus suorakaiteen muotoisenaTrapezium lasketaan toisella menetelmällä. Tämä parametri on yhtä suuri kuin toisen puolen pituuden tuote ja siihen viereisen terävän kulman viilto. Samoissa tapauksissa, kun kulman arvo on tuntematon, merkitään pienin sivupuoli puolisuunnikkaan korkeuteen ja lasketaan se Pythagoraanin lauseen mukaan. Pienimmän sivun suorakaiteen muotoinen puolisuunnikas löytyy kosini-ilmiöstä: c² = a² + b²-2ab * cosα; missä a, b, c edustavat kolmion sivuja; α on sivun a ja b välinen kulma.

opetus

1

Kolmesta kolmesta korkeudesta,joka laskee kuvan suurimpaan sivuun. Nähdäksesi tämän, ilmaise kaikki kolme kolmiota korkeutta sivujen mittojen kautta ja vertaile niitä. Oletetaan, että sivu a on mielivaltaisen akuutin kulman kolmesta sivusta a, b, c, sivu c on pienin. Osoitamme sivulle a, hb korkeuden h, sivulle b, korkeus sivulle c. Korkeus jakaa minkä tahansa kolmion kahteen suorakulmaiseen kolmioon, jossa tämä korkeus on aina yksi jalkoista.

2

Korkeus ha, vedetty suurimman puolen a,voidaan määrittää Pythagoras-lauseella: hа² = b² - а ² tai hа² = с² - а²². Jos a ja a2 ovat segmenttejä, joihin sivu a jakautuu korkeusha. Myös Pythagoraanin lause ilmaisee kahden muun kolmion korkeudet sen sivujen kautta: hb ² = a2-b1² tai hb² = c²-b2²; hc² = a2-c2 tai hc2 = b2-c2².

3

Korkeuksien määrittämiseen käytettävien kaavojen vertailustakolmio, on ilmeistä, että suhde minuend ja vähentäjä antaa pienimmän eron suhteen ha² = b² - a₁² ja ha² = s²-a₂² kuten vähennykseen a x ja a₂ - suurin sivujen pituudet kolmio.

4

Voit määrittää pienemmän kolmion korkeudenmyös kolmion tunnetun kulman viereen. Jos ehto asettaa useimmat kulmat, niin tämä kulma on vasten korkein käsi, ja juuri siksi se katsoi pienin korkeus. Välttäen monimutkaisia ​​laskelmia, paremmin ilmaista haluttu korkeus kautta trigonometriset funktiot kahden muun kulmat kolmion, koska suhde kolmiota sini vastakkaisen kulman - arvo tietylle kolmio on vakio. Näin ollen, pienin kolmio korkeus ha = b * SinB tai ha = c * sinc, jossa B on kulma suurin puolella ja puoli b, ja C - välinen kulma korkeimman puolella ja sivulta ja kolmio.