Vihje 1: Miten löytää oikea kuusikulmainen puoli
Vihje 1: Miten löytää oikea kuusikulmainen puoli
Kuusikulmainen - "kuusikulmainen" - muoto on,esimerkiksi pähkinöiden ja lyijykynät, hunajakenno- ja lumihiutaleet. Tämän lomakkeen oikeilla geometrisilla kuvilla on tietty ominaisuus, joka erottaa ne muista tasomuodoista. Se koostuu siitä, että ympyrän ympyrän säde on heksadesimaalilla yhtä suuri kuin sen sivun pituus - monissa tapauksissa tämä yksinkertaistaa huomattavasti monikulmion parametrien laskemista.

opetus
1
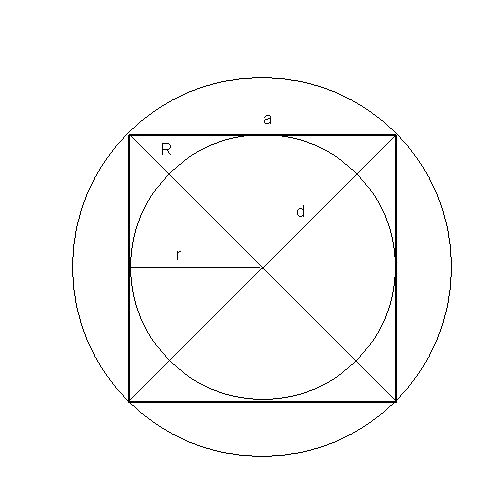
Jos ongelmaolosuhteissa säde (R) on kuvattu lähelle oikeaa kuusikulmio ympyrä laskee mitään - tämä arvo on sama kuin sivujen pituus (t) heks: t = R. Tunnetussa halkaisijat (D) yksinkertaisesti jakaa sen kahteen osaan: t = D / 2.
2
Oikeanpuoleinen kehä (P) kuusikulmio antaa meille mahdollisuuden laskea puolen (t) pituus yksinkertaisella jakooperaatiolla. Jakajana käytä sivujen lukumäärää, ts. kuusi: t = P / 6.
3
Säde (r), joka on merkitty tällaiseen monikulmioksiympyrä on sidottu sivun (t) pituuteen hieman monimutkaisemmalla kertoimella - kaksinkertaista säde ja jakaa tulos kolminkertaisen neliöjuuren kanssa: t = 2 * r / √3. Sama kaava kirjoitetun ympyrän halkaisijan (d) avulla muuttuu vielä matemaattisemmaksi: t = d / √3. Esimerkiksi, jonka säde on 50 cm, sivun pituus kuusikulmio tulisi olla suunnilleen 2 * 50 / √3 ≈ 57,735 cm.
4
Tunnettu alue (S) monikulmion kuudestapisteiden mahdollistaa myös laskea pituus sen puolella (t), mutta numeerinen liittyvä kerroin niitä tarkasti ilmaistuna osa kolme kokonaislukuja. Kaksi kolmasosaa jakamalla neliöjuuren kolme, ja saatu arvo neliöjuuren: t = √ (2 * S / (3 * √3)). Esimerkiksi, jos kuvion ala on 400 cm, sen sivun pituus tulisi olla noin √ (2 * 400 / (3 * √3)) ≈ √ (800/5196) ≈ √153,965 ≈ 12408 cm.
5
Ympyrä (L) on ympäröity oikealta kuusikulmio, liittyy säteeseen ja siten sivun pituuteen(t) lukumäärällä Pi. Jos se annetaan ongelman olosuhteissa, jaa sen arvo kahdella luvulla Pi: t = L / (2 * π). Jos tämä arvo on esimerkiksi 400 cm, sivun pituuden tulisi olla noin 400 / (2 * 3 142) = 400 / 6,284 ≈ 63,654 cm.
6
Sama parametri (l) kirjoitetulle ympyrälle mahdollistaa sivun pituuden laskemisen kuusikulmio (t) laskemalla sen ja tuotteen Pi: n tuotteen välinen suhde kolminkertaisen neliöjuuren kanssa: t = l / (π * √3). Esimerkiksi, jos kirjasinpiirin pituus on 300 cm, sivu kuusikulmio tulisi olla suunnilleen yhtä suuri kuin 300 / (3 142 * √3) ≈ 300 / (3 142 * 1,732) ≈ 300 / 5,442 ≈ 55,127 cm.
Vihje 2: Miten löytää kuusikulmion alue
Määritelmän mukaan planimetria on oikeamonikulmio on nimeltään monikulmio, jossa sivut ovat yhtä suuria ja kulmat ovat myös yhtä suuret. Säännöllinen kuusikulmio on säännöllinen monikulmio, jossa on useita sivuja yhtä suuri kuin kuusi. Säännöllisen monikulmion alueen laskemiseen on useita kaavoja.

opetus
1
Jos ympyrän säde on kuvattu lähellemonikulmio, pinta-ala voidaan laskea seuraavalla kaavalla: S = (n / 2), • R • sin (2π / n), jossa n - määrä monikulmion sivut, R - säde ympyrän, π = 180º.V säännöllinen kuusikulmio kaikki kulmat ovat yhtäläiset 120 °, niin kaava on muotoa: S = √3 * 3/2 * R

2
Tapauksessa, jossa ympyrä, jonka säde r on kirjoitettumonikulmio, sen pinta-ala lasketaan kaavalla: S = n * r² * tg (π / n), jossa n - määrä monikulmion sivut, r - säde piirretyn ympyrän, π = 180º.Dlya kuusikulmio, tämä kaava tulee: S = 2 * √ 3 * r²
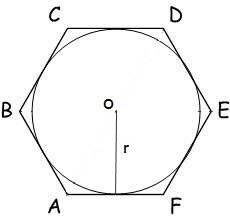
3
Säännöllisen monikulmion alue voi olla myöslaskea, tietäen vain pituus sen puolelta, jolla on kaava: S = n / 4 * a² * CTG (π / n), n - määrä monikulmion sivut, a - sivun pituus, monikulmio, π = 180º.Sootvetstvenno ala kuusikulmio on: S = √3 * 3/2 * a²

Vihje 3: Miten löytää todellinen poikkileikkausarvo
Tilojen ominaisuuksia avaruudessa on tällainen geometrian osio, kuten stereometria. Menetelmä on tärkein menetelmä stereometrian ongelmien ratkaisemisessa jakso Polyhedra. Sen avulla voit rakentaa oikein jakso polyhedra ja määritellä näiden osien muoto.

opetus
1
Määritelmä jakso mikä tahansa luku, eli sen luonnollinen arvo jakso, on usein epäselvä ongelmien muotoilussa kaltevan rakenteen rakentamisessa jakso. Kaltevaa osaa kutsutaan oikeutetusti etuprojektoriseksi sekanttikuvaksi. Ja rakentaa luonnollinen arvo riittää tekemään useita toimia.
2
Käytä viivainta ja kynää piirrä muoto sisään3 uloketta - edestä, ylhäältä ja sivulta katsottuna. Pääulokkeella, etukuvanäkymässä, näytä polku, jota pitkin etuprojektorikohtainen taso kulkee, ja josta piirrät viistoja.
3
Kaltevalla viivalla merkitään pääkohdat: tapahtumapaikat jakso ja poistua jakso. Jos muoto on suorakulmio, niin pisteitätulo ja poistuminen ovat yksi kerrallaan. Jos kuva on prisma, pistemäärä kaksinkertaistuu. Kaksi pistettä määrittää muodon ja poistumisen. Muut kaksi määrittävät pisteitä prisman sivuilla.
4
Sekoita mielivaltaisella etäisyydellä suora viiva,joka on yhdensuuntainen etuprojektorin kanssa. Sitten, pisteiden välillä, joka sijaitsee akselilla päätasolla piirtää viittaus ovat kohtisuorassa kalteva suora viiva, kunnes ne leikkaavat rinnakkain akselin. Näin saat projektio mittapisteissä lukuja uudessa koordinaatistossa.
5
Määritä muodon leveys ohittamalla suorat viivatpääkuvan päistä ylhäältä katsottuna. Merkitse vastaavilla indekseillä pisteiden ulokkeet linjan ja kuvion jokaisen leikkauspisteen kohdalle. Esimerkiksi, jos kohta A kuuluu päätasolle kuvion, pisteet A 'ja A "Belong ulkoneva konetta.
6
Aseta uusi koordinaattijärjestelmä syrjään,joka muodostuu pääpisteiden pystysuorien ulkonemien välillä. Rakennuksen tuloksena saatu luku on luonnollisen kaltevan arvon arvo jakso.