Vihje 1: Miten löytää kahden kaavion leikkauspisteen
Vihje 1: Miten löytää kahden kaavion leikkauspisteen
Jokainen erityinen aikataulu määritellään vastaavalla funktiolla. Prosessin löytäminen (useita kohtia) risteys kaksi kaavioita vähentää ratkaisemiseksi yhtälöt muoto f1 (x) = f2 (x), jonka päätös tulee haluttuun kohtaan.

Tarvitset
- - paperi;
- - kahva.
opetus
1
Jo matematiikan koulun kurssista oppilaat tulevat tietoisiksi mahdollisten pisteiden määrästä risteys kaksi kaavioita riippuu suoraan toiminnotyypistä. Esimerkiksi lineaarisilla funktioilla on vain yksi piste risteys, lineaarinen ja neliö - kaksi, neliö - kaksi tai neljä jne.
2
Yleisessä tapauksessa on kaksi lineaarista toimintoa (ks. Kuva 1). Olkoon y1 = k1x + b1 ja anna y2 = k2x + b2. Löytää piste niiden risteys on tarpeen ratkaista yhtälö y1 = y2 tai K1X + b1 = k2x + b2.Preobrazovav tasa saat: K1X-k2x = b2-b1.Vyrazite x seuraavasti: X = (B2-B1) / (K1-K2).
3
Kun löydettiin x: n arvo, pisteen koordinaatit risteys kaksi kaavioita abscissa-akselilla (0x-akseli), koordinaatti on edelleen laskettava koordinaattiakselin suuntaisesti (0Y-akseli). Tätä varten on välttämätöntä korvata x: n arvo mille tahansa toiminnolle risteys y1 ja y2 on seuraavat koordinaatit: ((b2-b1) / (k1-k2); k1 (b2-b1) / (k1-k2) + b2).
4
Analysoi esimerkki pisteen sijainnin laskemisesta risteys kaksi kaavioita (katso kuva 2) piste risteys kaavioita funktiot f1 (x) = 0,5x ^ 2 ja f2 (x) = 0,6x + 1,2.Tasoittamalla f1 (x) ja f2 (x) saadaan seuraava tasaus: 0.5x ^ = 0.6x + 1.2. Kun kaikki termit siirretään vasemmalle puolelle, saadaan muodon kvadraattinen yhtälö: 0.5x ^ 2 -0.6x-1.2 = 0. Tämän yhtälön ratkaisu on kaksi x: x1≈2, 26, x2≈-1,06: n arvoa.
5
Korvaa x1: n ja x2: n arvot jollakin funktio-ilmaisusta. Esimerkiksi, ja f_2 (x1) = 0,6 • 2,26 + 1,2 = 2,55, f_2 (x2) = 0,6 • (-1,06) + 1,2 = 0,56.Itak, Tarvittavat pisteet ovat: tA (2,26, 2,55) ja t.V (-1,06, 0,56).
Vihje 2: Miten löytää funktion kuvaajan leikkauspisteiden koordinaatit
Funktion y = f (x) kaavio on kaikkien joukkopisteitä, joiden koordinaatit x täyttävät suhteen y = f (x). Toiminnon kaavio kuvaa selvästi toiminnon käyttäytymistä ja ominaisuuksia. Graafin rakentamiseksi valitsemme yleensä useita argumentin x arvoja ja lasketaan niille funktion y = f (x) vastaavat arvot. Graafin tarkemman ja graafisen kaavion tekeminen on hyödyllistä löytää leikkauspisteet koordinaattiakseleilla.
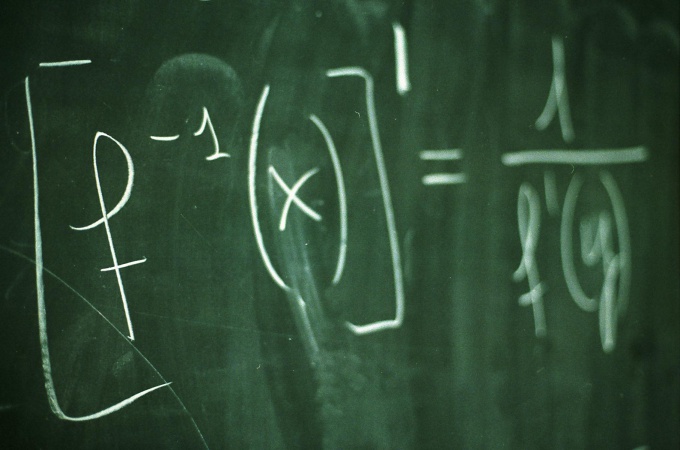
opetus
1
Funktion kuvaajan leikkauspisteen löytämineny-akselilla, on tarpeen laskea funktion arvo x = 0, ts. Etsi f (0). Käytetään esimerkiksi kuvassa 1 esitettyä lineaaritoimintoa kuvaava graafi. Sen arvo x = 0 (y = a * 0 + b) on b, joten kaavio leikkaa y-akselin pisteessä (0, b).

2
Abskissa (X-akselilla)toiminto on 0; y = f (x) = 0. X: n laskemiseksi on välttämätöntä ratkaista yhtälö f (x) = 0. Lineaarisen funktion tapauksessa saadaan yhtälö ax + b = 0, josta löydämme x = -b / a. Tällöin X-akseli leikkaa pisteessä (-b / a, 0).
3
Monimutkaisemmissa tapauksissa, esimasteen riippuvuus arvon X, yhtälön f (x) = 0 on kaksi juuret vuoksi x-akseli leikkaa kaksi kertaa. Jos jaksollinen funktio y x, esimerkiksi y = sin (x), sen kuvaaja on ääretön määrä leikkauspisteessä akselin H.Dlya validointi löytää koordinaatit kuvaaja leikkauspisteet X-akseli on tarpeen korvata löydetyt arvot x ilmaisun f (x) . Ilmaisun arvon mille tahansa laskennalliselle x: lle on oltava 0.
Vihje 3: Miten löytää toiminnon leikkauspisteet?
Ennen kuin tutkitaan toiminnan käyttäytymistä, on tarpeen määrittää harkittujen määrien vaihteluväli. Oletetaan, että muuttujat kuuluvat todellisiin numeroihin.

opetus
1
Toiminto on riippuvainen muuttujastaargumentin arvo. Argumentti on muuttuva riippumaton. Vaihteluvälit argumentin kutsutaan domeenin hyväksyttävien arvojen (DHS). Käyttäytyminen toiminnot pidetään rajoissa DHS, koska tällä alueella, suhde kahden muuttujan ei ole kaoottinen, mutta on tietyt säännöt ja voidaan kirjoittaa muodossa matemaattinen lauseke.
2
Harkitse mielivaltaista funktionaalista riippuvuutta F = φ (x), missä φ on matemaattinen ilmentymä. Toiminnolla voi olla koordinaattiakseleiden tai muiden toimintojen leikkauspisteitä.
3
Toiminnan risteyksissä abskissan kanssafunktio nollaksi: F (x) = 0. Ratkaise tämä yhtälö. Saat tietyn toiminnon leikkauspisteiden koordinaatit akselin OX kanssa. Tällaiset kohdat ovat yhtä monta kuin yhtälön juuret tietyn osan argumentin muutoksesta.
4
Toimiston leikkauspisteessä koordinaattiakselin kanssaargumentin arvo on nolla. Näin ollen ongelma muuttuu funktion arvon löytämiseksi x = 0: lle. OY-akselin toiminnon leikkauspisteet ovat yhtä monta kuin tietyn funktion arvot, joilla on nolla-argumentti.
5
Tietyn toiminnon leikkauspisteiden löytäminenjossa toinen funktio on tarpeen ratkaista yhtälöryhmä: Tässä φ (x) on lauseke, joka kuvaa tiettyä funktiota F, ψ (x) on ilmaus, joka kuvaa funktion W, risteyskohdan, jolle annetaan toimintoja on löydettävä. On ilmeistä, että risteyskohdissa molemmissa funktioissa käytetään samoja arvoja argumenttien yhtä suurille arvoille. Yhteiset kohdat kahdelle funktiolle ovat yhtä monta kuin yhtälöjärjestelmän ratkaisut tietyllä osalla argumentin muunnelmasta.
Vihje 4: Miten löytää toiminnot leikkauspisteistä
Risteyspisteissä funktioilla on samat arvot argumentin samalle arvolle. Etsi funktioiden leikkauskohdat, jotta määritettäisiin yhteisten pisteiden koordinaatit risteäville funktioille.

opetus
1
Yleisessä muodossa ongelmana on leikkauspisteiden löytäminenXOY-tasossa yhden argumentin Y = F (x) ja Y1 = F1 (x) funktiot vähenevät yhtälön Y = Y1 ratkaisemiseksi, koska yhteisessä pisteessä funktioilla on yhtäläiset arvot. X: n arvot, jotka täyttävät tasa-arvon F (x) = F1 (x), (jos ne ovat olemassa) ovat tiettyjen toimintojen risteyspisteiden abscisaaleja.
2
Jos toiminnot annetaan yksinkertaisella matemaattisellailmaisu ja riippuvat yhdestä argumentista x, niin leikkauspisteiden löytämisen ongelma voidaan ratkaista graafisesti. Määritä funktioiden kuvaajat. Määritä leikkauspisteiden koordinaattiakselit (x = 0, y = 0). Määritä useita muita argumentin arvoja, etsi funktion vastaavat arvot ja lisää pisteille saadut pistet. Mitä enemmän pisteitä käytetään rakentamiseen, sitä tarkempi kuvaaja on.
3
Jos funktion kaaviot leikkaavat, määritäristeyskohtien koordinaatit. Vahvista korvata nämä koordinaatit kaavoissa, jotka määrittelevät toiminnot. Jos matemaattiset lausekkeet ovat oikein, risteyspisteet löytyvät oikein. Jos funktiokaaviot eivät ole päällekkäisiä, kokeile muuttaa asteikkoa. Tee askel rakennuspisteiden välillä tarkemmin, jotta määriteltäisiin mikä osa numeerista tasoa kaavion linjat lähestyvät. Sitten määritetylle risteysalueelle luodaan yksityiskohtaisempi kaavio, jossa on pieni askel tarkasti määrittämään leikkauspisteiden koordinaatit.
4
Jos haluat löytää toiminnon leikkauspisteet, ei oletasossa ja kolmiulotteisessa tilassa, on otettava huomioon kahden muuttujan funktiot: Z = F (x, y) ja Z1 = F1 (x, y). Jotta voidaan määrittää funktioiden pisteiden koordinaatit, on välttämätöntä ratkaista yhtälöjärjestelmä, jossa on kaksi tuntematonta x ja y Z = Z </ s>.







